Summary:In order to evaluate the generalization ability of the model, that is, to judge whether the model is good or bad, we need to use a certain index to measure it. With the evaluation index, we can compare the pros and cons of different models, and use this index to further optimize the model.
This article is shared from Huawei Cloud Community “Detailed Explanation of Evaluation Indicators and Code Implementation of Target Detection Model”, author: Embedded Vision.
foreword
In order to understand the generalization ability of the model, that is, to judge whether the model is good or bad, we need to use a certain index to measure it. With the evaluation index, we can compare the pros and cons of different models, and use this index to further optimize the model.For classification and regression supervised models, each has its own evaluation criteria.
Different problems and different data sets will have different model evaluation indicators, such as classification problems. In the case of balanced data set categories, accuracy can be used as an evaluation indicator, but in reality, almost all data sets are unbalanced categories, so Generally, AP is used as the evaluation index of classification, and the AP of each category is calculated separately, and then mAP is calculated..
1. Precision, recall and F1
1.1, accuracy rate
Accuracy (precision) – Accuracythe percentage of correctly predicted results in the total samples, defined as follows:
Accuracy=(TP+TN)/(TP+TN+FP+FN)
Error rate and precision, although commonly used, do not meet all task requirements. Take the watermelon problem as an example. Assuming that the melon farmer brings a cart of watermelons, we use the trained model to discriminate the watermelons. Now the accuracy can only measure how many watermelons are judged to be of the correct category (two categories: good melons and bad melons). ). But if we are more concerned about “what proportion of the picked watermelons are good melons”, or “how many proportions of all good melons are picked”, then the indicators of accuracy and error rate are obviously not enough.
Although the accuracy rate can judge the overall correct rate, it cannot be used as a good indicator to measure the result when the sample is unbalanced. To give a simple example, for example, in a total sample, positive samples account for 90%, negative samples account for 10%, and the samples are seriously unbalanced. In this case, we only need to predict all samples as positive samples to get a high accuracy rate of 90%, but in fact we didn’t classify them very carefully, just casually. This shows that due to the problem of sample imbalance, the obtained high-accuracy results contain a lot of water. That is, if the samples are not balanced, the accuracy rate will be invalid.
1.2, precision rate, recall rate
The calculation of precision rate (precision rate) P and recall rate (recall rate) R involves the definition of confusion matrix. The confusion matrix table is as follows:
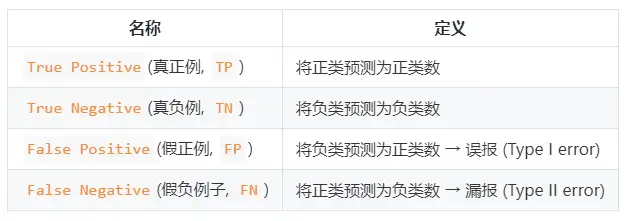
Precision and recall formulas:
- Precision rate (precision rate) P=TP/(TP+FP)P=TP/(TP+FP)
- Recall rate (recall rate) R=TP/(TP+FN)R=TP/(TP+FN)
Precision rate and accuracy rate look somewhat similar, but they are two completely different concepts.The precision rate represents the accuracy of the prediction in the positive sample results, and the accuracy rate represents the overall prediction accuracyincluding both positive and negative samples.
Accuracy describes how accurate the model isthat is, how many of the predicted positive examples are true examples;Recall describes how comprehensive the model is, that is, among the true samples, how many are predicted as positive by our model.The difference between precision and recall is thatdifferent denominatorone denominator is the number of samples predicted to be positive, and the other is the number of all positive samples in the original sample.
1.3, F1 score
if you want to find P and R A balance point between the two, we need a new indicator:f1 point.f1 The score takes both the precision rate and the recall rate into account, so that the two can reach the highest at the same time, and a balance is taken.f1 The calculation formula is as follows:
here f1 The calculation is for the binary classification model, multi-classification tasks f1 calculation see below.
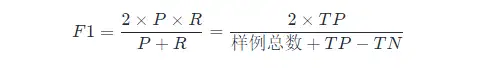
f1 The general form of a metric:Fβ, allowing us to express our bias towards precision/recall,FβThe calculation formula is as follows:
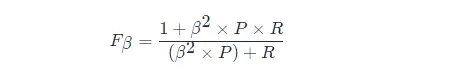
inbeta>1 has a greater impact on recall,beta<1 has a greater impact on precision.
Different computer vision problems have different preferences for the two types of errors, and often try to reduce the other type of errors when a certain type of error is not more than a certain threshold. In object detection,mAP(mean Average Precision) takes both errors into consideration as a unified indicator.
Many times we will have multiple confusion matrices, such as multiple training/testing, each time a confusion matrix can be obtained; or training/testing on multiple data sets, hoping to estimate the “global” performance of the algorithm; and Or perform multi-category tasks,Every two categoriesEach combination corresponds to a confusion matrix; … In general, we hope that in nno The precision rate and recall rate are comprehensively considered on a binary classification confusion matrix.
A direct approach is to calculate the precision and recall respectively on each confusion matrix, denoted as (P1,R1),(P2,R2),…,(Pn,n) Then take the average, so that you get “Macro Precision (Macro-P)”, “Macro Precision (Macro-R)” and the corresponding “Macro F1f1 (Macro-F1)”:
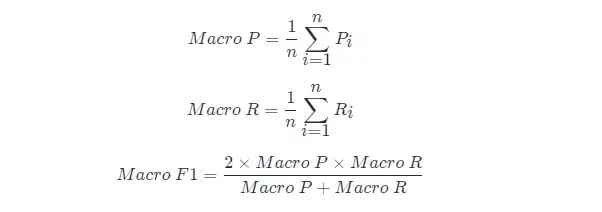
Another way is to average the corresponding elements of each confusion matrix to get TP, FP, TN, FNTP,FP,TN,FN and based on these averages, “Micro-Precision” (Micro-P), “Micro-Recall” (Micro-R) and “Micro-P” are calculated. f1″ (Mairo-F1)

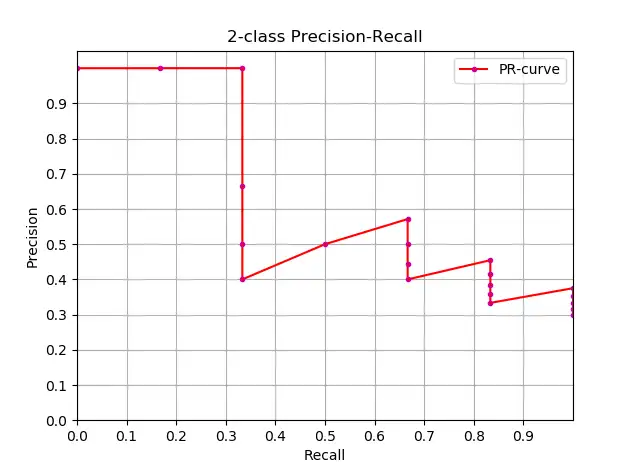
1.4, PR curve
The relationship between the precision rate and the recall rate can be shown by a PR graph, with the precision rate P as the vertical axis and the recall rate R as the horizontal axis, and the precision rate-recall rate curve is obtained, referred to as PR curve, the area under the PR curve is defined as AP:
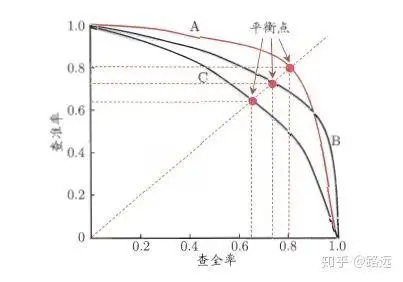
1.4.1, How to understand the PR curve
It can be understood from a ranking model or a classification model. Taking logistic regression as an example, the output of logistic regression is a probability number between 0 and 1. Therefore, if we want to judge whether a user is good or bad according to this probability, we must define a threshold. Generally speaking, the greater the probability of logistic regression, the closer it is to 1, which means that he is more likely to be a bad user. For example, we define a threshold of 0.5, that is, we consider all users with a probability less than 0.5 to be good users, and those with a probability greater than 0.5 to be considered bad users.Therefore, for the threshold value of 0.5, we can get the correspondinga pairPrecision and recall.
But the problem is: this threshold is defined arbitrarily by us, and we don’t know whether this threshold meets our requirements. Therefore, in order to find a most suitable threshold to meet our requirements, we must traverse all thresholds between 0 and 1, and each threshold corresponds to a pair of precision and recall, so we get PR curve.
Finally, how to find the best threshold point? First of all, we need to explain our requirements for these two indicators: we hope that both the precision rate and the recall rate are very high at the same time. But in fact, these two indicators are a pair of contradictions, and it is impossible to achieve double highs. It is obvious from the graph that if one of them is very high, the other must be very low. Selecting an appropriate threshold point depends on actual needs. For example, if we want a high recall rate, we will sacrifice some precision rate. In the case of ensuring the highest recall rate, the precision rate is not so low. .
1.5, ROC curve and AUC area
- The PR curve has Recall as the horizontal axis and Precision as the vertical axis; while the ROC curve has FPR as the horizontal axis and TPR as the vertical axis**.The closer the PR curve is to the upper right corner, the better the performance. Both metrics of the PR curve focus on positive examples
- The PR curve shows the Precision vs Recall curve, and the ROC curve shows the FPR (x-axis: False positive rate) vs TPR (True positive rate, TPR) curve.
- [ ] ROC curve
- [ ] AUC area
2. AP and mAP
2.1, Understanding of AP and mAP indicators
AP measures the quality of the trained model in each category, and mAP measures the quality of the model in all categories. After obtaining the AP, the calculation of mAP becomes very simple, which is to take the average of all APs . The calculation formula of AP is relatively complicated (so it is a separate chapter), please refer to the following for details.
The term mAP has different definitions. This metric is commonly used in the areas of information retrieval, image classification, and object detection. However, the two fields calculate mAP differently. Here we only talk about the mAP calculation method in object detection.
mAP is often used as an evaluation index for target detection algorithms. Specifically, for each picture detection model will output multiple prediction frames (far exceeding the number of real frames), we use IoU (Intersection Over Union) to Whether the prediction box of the mark prediction is accurate. After the marking is completed, with the increase of the prediction frame, the recall rate R will always increase,The accuracy rate P is averaged at different recall rates R levels to obtain the APand finally average all categories according to their proportions to get the mAP index.
2.2, Approximate calculation of AP
Knowing the definition of AP, the next step is to understand the realization of AP calculation. In theory, AP can be calculated by integral. The formula is as follows:
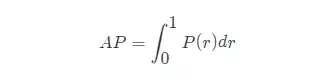
But usually, approximate or interpolation methods are used to calculate AP.
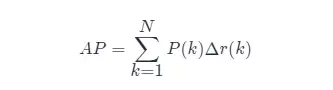
- Approximate calculation AP (approximate average precision), this calculation method is approximated form;
- It is obvious that point pairs lying on a vertical line calculate AP no contribution;
- here N is the total amount of data,k is the index of each sample point, Δr(k)=r(k)−r(k−1).
Approximate calculation The code for AP and PR curve drawing is as follows:
import numpy as np
import matplotlib.pyplot as plt
class_names = ["car", "pedestrians", "bicycle"]
def draw_PR_curve(predict_scores, eval_labels, name, cls_idx=1):
"""calculate AP and draw PR curve, there are 3 types
Parameters:
@all_scores: single test dataset predict scores array, (-1, 3)
@all_labels: single test dataset predict label array, (-1, 3)
@cls_idx: the serial number of the AP to be calculated, example: 0,1,2,3...
"""
# print('sklearn Macro-F1-Score:', f1_score(predict_scores, eval_labels, average="macro"))
global class_names
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(15, 10))
# Rank the predicted scores from large to small, extract their corresponding index(index number), and generate an array
idx = predict_scores[:, cls_idx].argsort()[::-1]
eval_labels_descend = eval_labels[idx]
pos_gt_num = np.sum(eval_labels == cls_idx) # number of all gt
predict_results = np.ones_like(eval_labels)
tp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend == cls_idx) # ndarray
fp_arr = np.logical_and(predict_results == cls_idx, eval_labels_descend != cls_idx)
tp_cum = np.cumsum(tp_arr).astype(float) # ndarray, Cumulative sum of array elements.
fp_cum = np.cumsum(fp_arr).astype(float)
precision_arr = tp_cum / (tp_cum + fp_cum) # ndarray
recall_arr = tp_cum / pos_gt_num
ap = 0.0
prev_recall = 0
for p, r in zip(precision_arr, recall_arr):
ap += p * (r - prev_recall)
# pdb.set_trace()
prev_recall = r
print("------%s, ap: %f-----" % (name, ap))
fig_label="[%s, %s] ap=%f" % (name, class_names[cls_idx], ap)
ax.plot(recall_arr, precision_arr, label=fig_label)
ax.legend(loc="lower left")
ax.set_title("PR curve about class: %s" % (class_names[cls_idx]))
ax.set(xticks=np.arange(0., 1, 0.05), yticks=np.arange(0., 1, 0.05))
ax.set(xlabel="recall", ylabel="precision", xlim=[0, 1], ylim=[0, 1])
fig.savefig("./pr-curve-%s.png" % class_names[cls_idx])
plt.close(fig)2.3, interpolation calculation AP
Interpolated average precision APAP The evolution process of the formula will not be discussed here. For details, please refer to this article. My formulas and diagrams here are also referred to this article. 11-point interpolation calculation method to calculate APAP The formula is as follows:
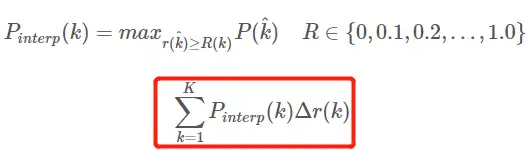
- This is the AP in the usual sense of 11 points_Interpolated form, select fixed 0,0.1,0.2,…,1.00,0.1,0.2,…,1.0 11 thresholds, this is used in PASCAL2007
- Here because only 11 points are involved in the calculation, so K=11, called 11 points_Interpolated,k is the threshold index
- Pinterp(k) take the k The maximum value in the sample after the sample point corresponding to the threshold, except that the threshold here is limited to 0,0.1,0.2,…,1.00,0.1,0.2,…,1.0.
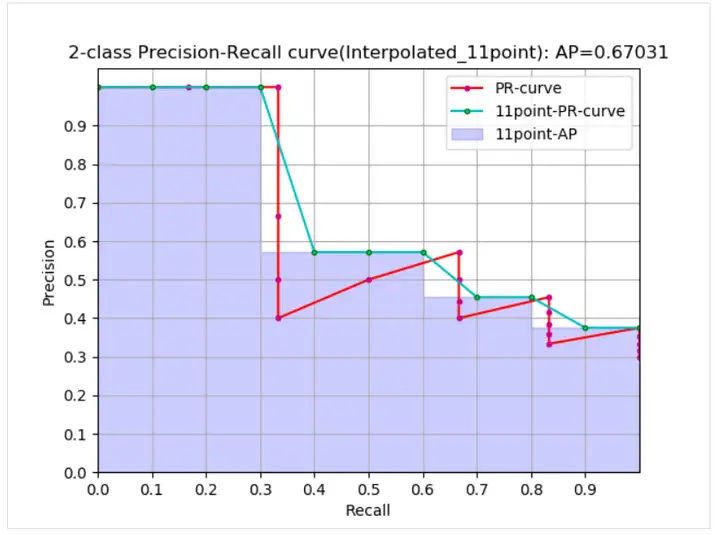
From the curve, the real AP< approximated AP < Interpolated AP, 11-points Interpolated AP may be large or small, and when the amount of data is large, it will be close to Interpolated AP. Unlike Interpolated AP, AP is calculated in the previous formula. It is the area estimate of the PR curve. The formula given in the PASCAL paper is simpler and more crude, directly calculating the average value of the precision at 11 thresholds. The 11-point formula for calculating AP given in the PASCAL paper is as follows.
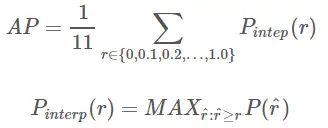
1. Calculate AP under the given conditions of recal and precision:
def voc_ap(rec, prec, use_07_metric=False):
"""
ap = voc_ap(rec, prec, [use_07_metric])
Compute VOC AP given precision and recall.
If use_07_metric is true, uses the
VOC 07 11 point method (default:False).
"""
if use_07_metric:
# 11 point metric
ap = 0.
for t in np.arange(0., 1.1, 0.1):
if np.sum(rec >= t) == 0:
p = 0
else:
p = np.max(prec[rec >= t])
ap = ap + p / 11.
else:
# correct AP calculation
# first append sentinel values at the end
mrec = np.concatenate(([0.], rec, [1.]))
mpre = np.concatenate(([0.], prec, [0.]))
# compute the precision envelope
for i in range(mpre.size - 1, 0, -1):
mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
# to calculate area under PR curve, look for points
# where X axis (recall) changes value
i = np.where(mrec[1:] != mrec[:-1])[0]
# and sum (\Delta recall) * prec
ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
return ap2. Calculate AP given target detection result file and test set label file xml:
def parse_rec(filename):
""" Parse a PASCAL VOC xml file
Return : list, element is dict.
"""
tree = ET.parse(filename)
objects = []
for obj in tree.findall('object'):
obj_struct = {}
obj_struct['name'] = obj.find('name').text
obj_struct['pose'] = obj.find('pose').text
obj_struct['truncated'] = int(obj.find('truncated').text)
obj_struct['difficult'] = int(obj.find('difficult').text)
bbox = obj.find('bndbox')
obj_struct['bbox'] = [int(bbox.find('xmin').text),
int(bbox.find('ymin').text),
int(bbox.find('xmax').text),
int(bbox.find('ymax').text)]
objects.append(obj_struct)
return objects
def voc_eval(detpath,
annopath,
imagesetfile,
classname,
cachedir,
ovthresh=0.5,
use_07_metric=False):
"""rec, prec, ap = voc_eval(detpath,
annopath,
imagesetfile,
classname,
[ovthresh],
[use_07_metric])
Top level function that does the PASCAL VOC evaluation.
detpath: Path to detections result file
detpath.format(classname) should produce the detection results file.
annopath: Path to annotations file
annopath.format(imagename) should be the xml annotations file.
imagesetfile: Text file containing the list of images, one image per line.
classname: Category name (duh)
cachedir: Directory for caching the annotations
[ovthresh]: Overlap threshold (default = 0.5)
[use_07_metric]: Whether to use VOC07's 11 point AP computation
(default False)
"""
# assumes detections are in detpath.format(classname)
# assumes annotations are in annopath.format(imagename)
# assumes imagesetfile is a text file with each line an image name
# cachedir caches the annotations in a pickle file
# first load gt
if not os.path.isdir(cachedir):
os.mkdir(cachedir)
cachefile = os.path.join(cachedir, '%s_annots.pkl' % imagesetfile)
# read list of images
with open(imagesetfile, 'r') as f:
lines = f.readlines()
imagenames = [x.strip() for x in lines]
if not os.path.isfile(cachefile):
# load annotations
recs = {}
for i, imagename in enumerate(imagenames):
recs[imagename] = parse_rec(annopath.format(imagename))
if i % 100 == 0:
print('Reading annotation for {:d}/{:d}'.format(
i + 1, len(imagenames)))
# save
print('Saving cached annotations to {:s}'.format(cachefile))
with open(cachefile, 'wb') as f:
pickle.dump(recs, f)
else:
# load
with open(cachefile, 'rb') as f:
try:
recs = pickle.load(f)
except:
recs = pickle.load(f, encoding='bytes')
# extract gt objects for this class
class_recs = {}
npos = 0
for imagename in imagenames:
R = [obj for obj in recs[imagename] if obj['name'] == classname]
bbox = np.array([x['bbox'] for x in R])
difficult = np.array([x['difficult'] for x in R]).astype(np.bool)
det = [False] * len(R)
npos = npos + sum(~difficult)
class_recs[imagename] = {'bbox': bbox,
'difficult': difficult,
'det': det}
# read dets
detfile = detpath.format(classname)
with open(detfile, 'r') as f:
lines = f.readlines()
splitlines = [x.strip().split(' ') for x in lines]
image_ids = [x[0] for x in splitlines]
confidence = np.array([float(x[1]) for x in splitlines])
BB = np.array([[float(z) for z in x[2:]] for x in splitlines])
nd = len(image_ids)
tp = np.zeros(nd)
fp = np.zeros(nd)
if BB.shape[0] > 0:
# sort by confidence
sorted_ind = np.argsort(-confidence)
sorted_scores = np.sort(-confidence)
BB = BB[sorted_ind, :]
image_ids = [image_ids[x] for x in sorted_ind]
# go down dets and mark TPs and FPs
for d in range(nd):
R = class_recs[image_ids[d]]
bb = BB[d, :].astype(float)
ovmax = -np.inf
BBGT = R['bbox'].astype(float)
if BBGT.size > 0:
# compute overlaps
# intersection
ixmin = np.maximum(BBGT[:, 0], bb[0])
iymin = np.maximum(BBGT[:, 1], bb[1])
ixmax = np.minimum(BBGT[:, 2], bb[2])
iymax = np.minimum(BBGT[:, 3], bb[3])
iw = np.maximum(ixmax - ixmin + 1., 0.)
ih = np.maximum(iymax - iymin + 1., 0.)
inters = iw * ih
# union
uni = ((bb[2] - bb[0] + 1.) * (bb[3] - bb[1] + 1.) +
(BBGT[:, 2] - BBGT[:, 0] + 1.) *
(BBGT[:, 3] - BBGT[:, 1] + 1.) - inters)
overlaps = inters / uni
ovmax = np.max(overlaps)
jmax = np.argmax(overlaps)
if ovmax > ovthresh:
if not R['difficult'][jmax]:
if not R['det'][jmax]:
tp[d] = 1.
R['det'][jmax] = 1
else:
fp[d] = 1.
else:
fp[d] = 1.
# compute precision recall
fp = np.cumsum(fp)
tp = np.cumsum(tp)
rec = tp / float(npos)
# avoid divide by zero in case the first detection matches a difficult
# ground truth
prec = tp / np.maximum(tp + fp, np.finfo(np.float64).eps)
ap = voc_ap(rec, prec, use_07_metric)
return rec, prec, ap2.4, mAP calculation method
because mAP Values are calculated for all categories in the dataset AP values are averaged, so we have to calculate mAPwe must first know a certain category of AP How to find the value.A certain category of different data sets AP There are three main calculation methods:
(1) In VOC2007, only need to select when Recall>=0,0.1,0.2,…,1recall>=0,0.1,0.2,…,1 The maximum value of Precision when there are 11 points in total, then APAP It is the average of these 11 Precisions, mAPmAP That is, all categories of APAP the average of the values. Centralized calculation of AP for VOC dataAP the code(Using the interpolation calculation method, the code comes frompy-faster-rcnn repository)
(2) In VOC2010 and later, it is necessary to select the maximum value of Precision greater than or equal to these Recall values for each different Recall value (including 0 and 1), and then calculate the area under the PR curve as AP value, mAPmAP is all categories AP the average of the values.
(3) For the COCO data set, set multiple IOU thresholds (0.5-0.95, 0.05 is the step size), and there is a certain category of AP value under each IOU threshold, and then calculate the AP average under different IOU thresholds, that is The desired final AP value of a category.
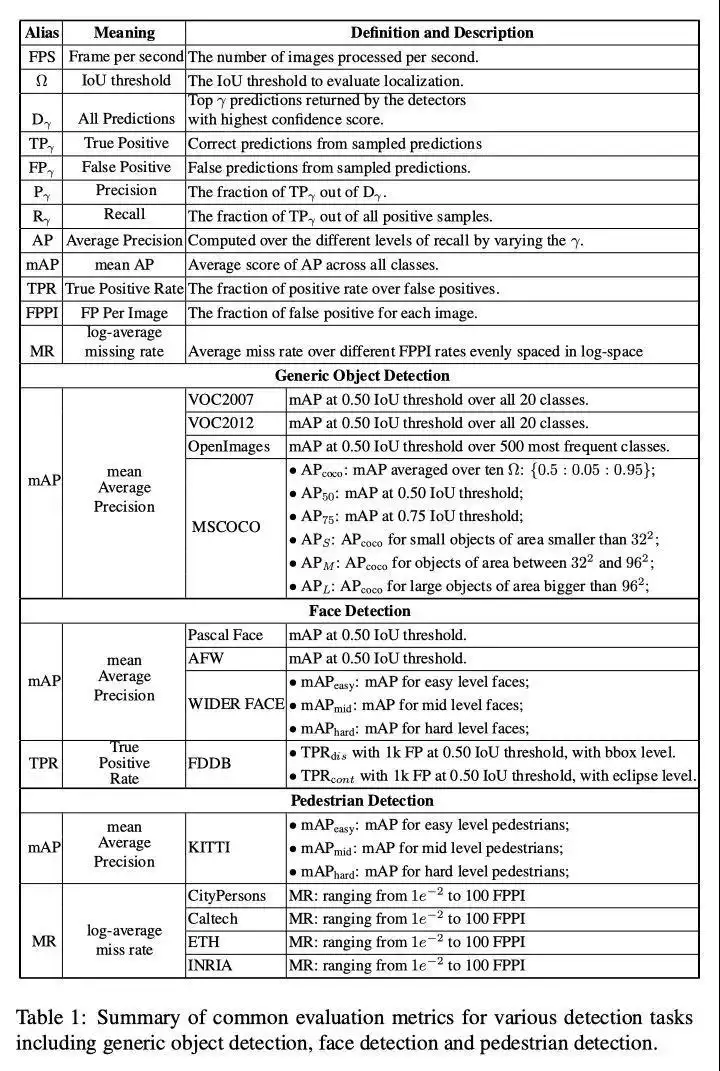
3. Summary of Target Detection Metrics
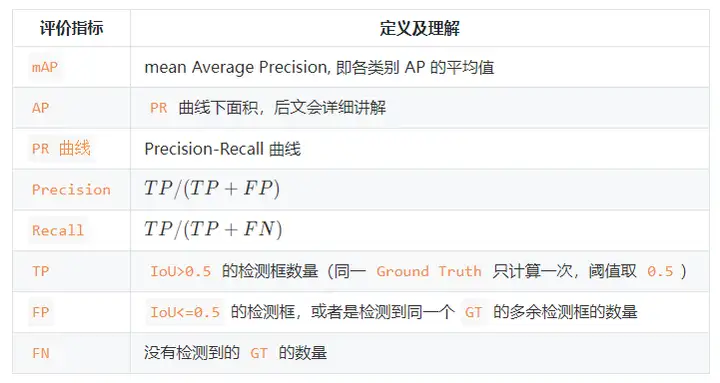
Fourth, reference materials
Click to follow and learn about Huawei Cloud’s fresh technologies for the first time~
#Detailed #explanation #evaluation #index #code #implementation #target #detection #model #HUAWEI #CLOUD #Developer #Alliances #personal #space #News Fast Delivery