This article mainly touches on the basics of graph machine learning.

We start by learning what a graph is, why a graph is used, and how to best represent a graph. Then, we briefly introduce how you can learn on graph data, from the previous methods of neural network (while we will explore graph features) to the now well-known graph neural network (Graph Neural Network, GNN). Finally, we’ll take a peek into the world of Transformers on graph data.

What is a graph?

Essentially, a graph describes entities linked to each other by relationships.

There are many examples of graphs in reality, including social networks (such as Twitter, mammoths, and any citation network linking papers and authors), molecules, knowledge graphs (such as UML diagrams, encyclopedias, and those with hyperlinks between pages). linked websites), sentences represented as syntax trees, 3D grids, etc. Therefore, it is no exaggeration to say that graphs are everywhere.

Entities in a graph (or network) are called node (or vertices), and the connections between them are called side (or link). For example, in a social network, nodes are users, and edges are connections between them; in molecules, nodes are atoms, and edges are molecular bonds between them.

• A graph in which more than one type of node or edge can exist is called heterogeneous graph (Example: There are two types of nodes in the reference network, papers and authors, and the edges of an XML graph containing multiple relationship types are multi-type). A heterogeneous graph cannot be characterized by its topology alone, it requires additional information. This article focuses on homogeneous graphs.

• Figure can also be Directed (For example, in a following network, A follows B, but B may not follow A) or undirected (such as in a molecule, the relationship between atoms is bidirectional). Edges can connect different nodes, or connect themselves (self-edges, self-edges), but not all nodes must have connections.

If you want to use your own data, first you have to think about how to best characterize it (homogeneous/heterogeneous, directed/undirected, etc.).

What are graphs for?

Let’s take a look at what tasks we can do on the map.

exist graph levelthe main tasks are:

• Graph generation, which can be used in drug discovery tasks to generate new possible drug molecules,
• Graph evolution (given a graph, predict how it will evolve over time), can be used in physics to predict the evolution of a system,
• Graph-level prediction (graph-based classification or regression tasks), such as predicting molecular toxicity.

exist node level, which is usually used to predict node attributes. For example, Alphafold uses the node attribute prediction method to predict the 3D coordinates of atoms given the molecular overall map, and thus predict how molecules fold in 3D space, which is a relatively difficult biochemical problem.

exist edge layer, we can do edge attribute prediction or missing edge prediction. Edge attribute prediction can be used to predict adverse side effects of drugs given a drug pair. Missing edge prediction is used in recommender systems to predict whether two nodes in a graph are related.

Another possible job is to subplot level , which can be used for community detection or subgraph attribute prediction. Social networks use community detection to determine how people are connected. We can find subgraph attribute prediction in travel systems such as Google Maps, where it is used to predict arrival times.

There are two ways to accomplish these tasks.

When you want to predict the evolution of a particular graph, you work in Direct push (transductive) mode, all training, verification and inference in transduction mode are based on the same graph.If this is your setup, be careful! It is not easy to create train/eval/test sets on the same graph. However, many tasks actually work on different graphs (different train/eval/test splits), which we call inductive model.

How to represent graph?

There are two commonly used methods for representing graphs for subsequent processing and manipulation:

• Expressed as a collection of all edges (and possibly a collection of all nodes for supplement).
• Or expressed as an adjacency matrix between all nodes. The adjacency matrix is ​​a $node_size \times node_size$ size square matrix, which indicates which nodes on the graph are directly connected (if $n_i$ and $n_j$ are connected, then $A_{ij} = 1$, otherwise it is 0) .

Note: most graphs are not densely connected, so their adjacency matrices are sparse, which makes computation difficult.

While these indications may look familiar, don’t be fooled!

Graphs are quite different from typical objects used in machine learning, as their topology is much more complex than sequences (such as text or audio) or ordered grids (such as images and videos): even though they can be represented as linked lists or matrices , but they cannot be treated as ordered objects.

What exactly does this mean? If you have a sentence, and you swap the word order of that sentence, you’ve created a new sentence. If you have an image, and you rearrange the columns of that image, you create a new image.

But the graph doesn’t do that. If you rearrange the edge list of the graph or the columns of the adjacency matrix, the graph remains the same graph (a more formal term is permutation invariance).

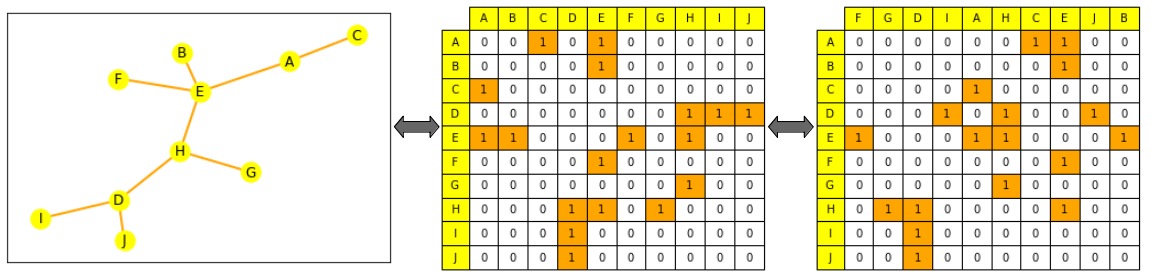
Graph representation based on machine learning

The general flow of processing graphs with machine learning is: first generate a meaningful representation for the objects you are interested in (nodes, edges, or full graphs, depending on your task), and then use them to train a predictor for the target task . As with other modal data, we want to impose some constraints on the mathematical representation of these objects such that similar objects are mathematically close. However, this similarity is difficult to strictly define in graph machine learning. For example, which two nodes with the same label or two nodes with the same neighbors are more similar?

Note: In subsequent sections, we will focus on how to generate node representations. Once you have a node-level representation, it’s possible to get edge or graph-level information. You can get edge-level information by concatenating the representations of the two nodes connected by the edge or by doing a dot product. As for the information at the graph level, it can be obtained by doing a global pooling (average, summation, etc.) on tensors concatenated from the representations of all nodes on the graph. Of course, doing this will smooth out or lose some information on the entire graph. It may be more reasonable to use iterative layered pooling, or add a virtual node connected to all other nodes on the graph, and then use its representation as the entire graph representation.

Neural Networks Previous Methods

Use only hand-designed features

Before the advent of neural networks, graphs and items of interest in graphs could be represented as combinations of features that were task-specific. These features are still used for data augmentation and semi-supervised learning, although more sophisticated feature generation methods now exist. At this time, your main job is to find the best features for subsequent network training according to the target task.

node level features Can provide information about its importance (how important is this node to the graph?) and/or structural (what is the shape of the graph around the node?), both can be combined.

node centrality Measures the importance of nodes in a graph. It can be calculated recursively, that is, the centrality of each node’s neighbor nodes is continuously summed until convergence, or it can be obtained by calculating the shortest distance between nodes, and so on.node degree Measures the number of direct neighbors of a node.Clustering coefficient Measures the degree to which a node’s neighbors are connected to each other.Graphlets degree vectors (GDV) Counts the number of distinct primitives for a given root node, where primitives are all sparklines that can be created with a given number of connected nodes (e.g. 3 connected nodes can generate a line with 2 edges, or a 3-edge triangle).

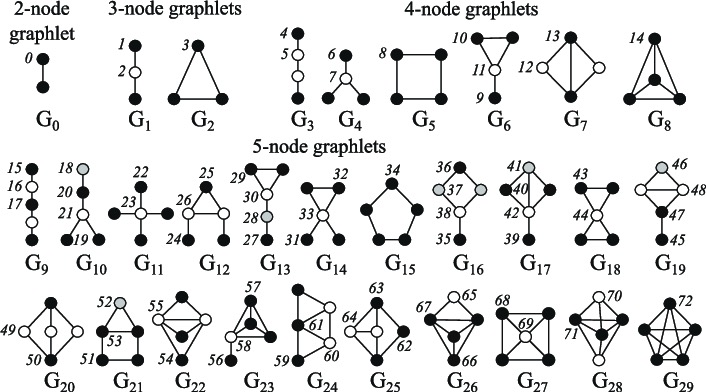
Edge-level features bring more detailed information about the connectivity between nodes, effectively supplementing the graph representation, including: the shortest distance between two nodes, their common neighbors, and their Katz index (represents the number of paths between two nodes whose length is less than a certain value, which can be directly calculated from the adjacency matrix).

Layer Features Contains high-level information about graph similarities and specifications.total number of primitives Although computationally expensive, provides information about the shape of the subgraph.kernel method The similarity between graphs is measured by different “bag of nodes” (similar to bag of words) methods.

walk-based method

walk-based method The similarity matrix is ​​defined using the likelihood of visiting node i from node j during a random walk; these methods combine local and global information. for example,Node2VecSimulate random walks between nodes in the graph, model these walk paths as skip-grams, which is very similar to how we process words in sentences, and then calculate embeddings. The method based on random walk can also be used to speed up the Page Rank method to help calculate the importance score of each node (for example: if the importance score is based on the connectivity of each node to other nodes, we can use The frequency of random walk visits to each node to simulate this connectivity).

However, these methods also have limitations: they cannot obtain new node embedding vectors, cannot capture the structural similarity between nodes well, and cannot use newly added features.

Graph neural network

Neural networks can generalize to unseen data. We have mentioned some graph representation constraints above, so what characteristics should a good neural network have?

it should:

• Permutation invariance is satisfied:

  • Equation: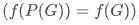where f is the neural network, P is the permutation function, and G is the graph.
  • Explanation: After the replaced image and the original image pass through the same neural network, their representation should be the same.

• Satisfy the substitution equivalence

  • formula: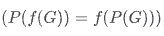also f is the neural network, P is the permutation function, and G is the graph.
  • Explanation: Replacing the graph first and then passing it to the neural network is equivalent to replacing the output graph representation of the neural network.

Typical neural networks such as recurrent neural networks (RNN) or convolutional neural networks (CNN) are not permutation invariant. Therefore, Graph Neural Network (Graph Neural Network, GNN) was introduced as a new architecture to solve this problem (initially used as a state machine).

A GNN consists of successive layers.A GNN layer passes through message passing The procedure represents a node as a combination of its neighbors and its own representation (aggregation), and then usually we also use an activation function to add some nonlinearity.

compared to other models: CNN can be regarded as a GNN with a fixed neighborhood (ie, sliding window) size and order, that is to say, CNN is not permutation equivalent. A Transformer model without positional embeddings can be viewed as a GNN working on a fully connected input graph.

Aggregation and Messaging

Various methods can be used to aggregate the messages of neighboring nodes, for example, there are summation, averaging and so on. Some notable jobs include:

• The graph convolutional network averages the normalized representations of all neighbors of the target node for aggregation (most GNNs are actually GCNs);
• The graph attention network will learn how to weight and aggregate neighboring nodes according to the importance of neighboring nodes (similar to the transformer model idea);
• GraphSAGE first samples neighboring nodes on different hops, and then uses the max pooling method to aggregate information based on the sampled subgraph in multiple steps;
• The graph isomorphic network first calculates the summation of the representations of neighboring nodes, and then sends it to an MLP to calculate the final aggregated information.

Choose aggregation method: Some aggregation techniques (especially mean pooling and max pooling) may fail when encountering similar nodes with only slight differences in neighboring nodes (for example: using mean pooling, a node has 4 Neighboring nodes, represented as 1, 1, -1, -1 respectively, become 0 after taking the mean value; and the other node has 3 neighboring nodes, represented as – 1, 0, 1 respectively, and are also 0 after taking the mean value. are indistinguishable.).

GNN shape and oversmoothing issues

Each time a new layer is added, more and more node information will be included in the node representation.

A node, at the first level, only aggregates information about its immediate neighbors. By the second level, they still aggregate only immediate neighbor information, but this time, the representations of their direct neighbors already contain their respective neighbor information (obtained from the first level). After n layers, the representation of all nodes becomes an aggregate of all their neighbors at distance n. If the diameter of the whole graph is less than n, the information of the whole graph is aggregated!

If your network has too many layers, there is a risk that each node aggregates the information of all nodes in the whole graph (and the representation of all nodes converges to the same value), which is called the oversmoothing problem (the oversmoothing problem) .

This can be solved by:

• When designing the number of layers of GNN, first analyze the diameter and shape of the graph, and the number of layers should not be too large to ensure that each node does not aggregate the information of the entire graph
• Add layer complexity
• Add a non-messaging layer to handle messages (such as a simple MLP layer)
• Increase skip-connections (skip-connections)

The over-smoothing problem is an important research area of ​​graph machine learning, because it prevents GNN from becoming larger, and models such as Transformers on other modal data have proved that making the model larger has a good effect.

Figure Transformers

The Transformer model without a positional encoding layer is permutation invariant, and the Transformer model has been proven to be very scalable, so recently everyone began to see how to transform Transformer to adapt to graph data (review). Most methods focus on how to best represent the graph, such as finding the best features, the best way to represent location information, and how to change the attention to adapt to this new data.

Here we collect some interesting work that, as of this writing, achieved state-of-the-art or near-state performance on one of the hardest existing benchmarks, the Stanford Open Graph Benchmark (OGB). result:

• Graph Transformer for Graph-to-Sequence Learning (Cai and Lam, 2020) introduce a graph encoder that represents a node as a concatenation of its own embeddings and positional embeddings, inter-node relations as the shortest paths between them, and then uses a relation-augmented self-attention Mechanisms combine the two.
• Rethinking Graph Transformers with Spectral Attention (Kreuzer et al, 2021) introduced Spectral Attention Networks (SANs). It combines node features with learned positional encodings (computed from Laplacian eigenvalues ​​and eigenvectors), uses these as attention keys and queries, and then uses edge features as attention Force values ​​(values).
• GRPE: Relative Positional Encoding for Graph Transformer (Park et al, 2021) introduced the graph-relative position encoding Transformer. It first combines node information in the position encoding at the graph level, and also combines node information in the position encoding at the edge level, and then further combines the two in the attention mechanism.
• Global Self-Attention as a Replacement for Graph Convolution (Hussain et al, 2021) introduced the edge augmentation Transformer. The architecture embeddings nodes and edges separately and aggregates them through a modified attention mechanism.
• Do Transformers Really Perform Badly for Graph Representation (Ying et al, 2021) introduced Microsoft’s Graphormer, the model won OGB #1 when it came out. This architecture uses node features as query/key/value (Q/K/V) for attention, and then combines these representations with centrality, spatial and edge encoding information by summation in the attention mechanism.

The latest work is Pure Transformers are Powerful Graph Learners (Kim et al, 2022), which introduces TokenGT. This approach represents the input graph as a sequence of node and edge embeddings (and augments it with orthonormal node identifiers and trainable type identifiers) instead of positional embeddings, and finally takes this sequence Input to the Tranformer model. Super simple, yet clever!

Slightly differently,Recipe for a General, Powerful, Scalable Graph Transformer (Rampášek et al, 2022) introduce not a model but a framework called GraphGPS. It allows combining message-passing networks and linear (long-range) transformer models to easily create a hybrid network. The framework also includes a number of tools for computing positional and structural encodings (at the node, graph, edge level), feature enhancement, random walks, and more.

Using transformer models on graph data is still a very nascent field, but it looks promising because it can alleviate some of the limitations of GNNs, such as scaling to larger/denser graphs, or increasing the model size without worrying oversmoothing problem.

more advanced resources

If you want to delve deeper, check out these courses:

• college course format
• video form
• related books

Good libraries for working with graph data are PyGeometric (for graph machine learning) and NetworkX (for more general graph operations).

If you need a good quality benchmark, you can try:

If you want more datasets, you can take a look at:

external image source

The emoji expressions in the thumbnails are from Openmoji (CC-BY-SA 4.0), and the pictures of the primitives are from Biological network comparison using graphlet degree distribution (Pržulj, 2007).

Original English text: https://huggingface.co/blog/intro-graphml

Translator: Matrix Yao